设置
快速交货
免运费
国际贸易术语
支付类型
市场产品
Inverse Kinematics: How Robots Move
2024-11-15 | By Antonio Velasco
It's easy to pick up objects off a desk, right? Just reach out, grab, and be on with your day. There's a lot that goes into that one simple motion, though. Your mind does unconscious calculations on how much to turn your joints or how far to extend your arm, and replicating such a motion in robotics can prove to be a bit tricky. When looking at it from a mathematical point of view, it can become much easier. Hence, introducing Inverse Kinematics allows us to give robots the gift of accurate motion.
An Example
Let's take this double-jointed robot arm as an example. First, let's simplify this example into a double-jointed arm:
In our example, we'll also just consider a 2D plane. Say that we want the endpoint of the arm (or the camera in the physical picture) to reach position (6,3). In order to do so, we're given two variables that we can change: Theta 1 and Theta 2 (or rather, the angles). We're also given two constraints: the lengths of each of the segments. These act as constraints as we cannot shorten or extend them and rather have to turn the joints to an appropriate point.
In a two-joint system in the 2D plane, this solution can be relatively easy. Essentially, we want to create a triangle between the goal point, our segments, and the origin. We're given two segments (or sides) and can determine the third one through a bit of math. The third segment would be the distance of the goal to the origin, found by the Pythagorean Theorem:
Now, we have 3 segments: 3m, 4m, and sqrt(45) or 6.7m. We can now calculate the angles of Theta 1 and Theta 2 with these constraints through trigonometry:
Theta 1: arctan(3/4) = 36.87 deg
Theta 2: 180 - arctan(3/4) - arctan(4/3) = 92 deg
As such, we have now solved for the angles and can apply it to our robot arm:
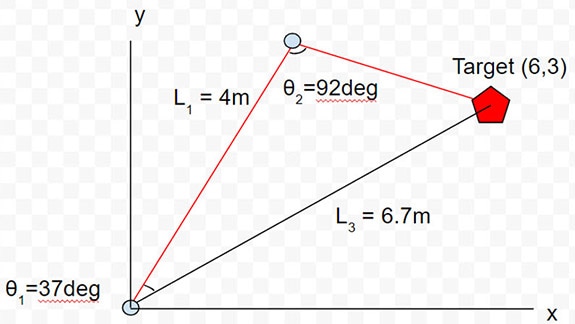
Now, we can see the final position of our robot arm. This type of math can easily be coded for the computer to calculate and can produce such results easily.
An edge case to this would be that there are two solutions to this problem:
This case utilizes the same angles and same lengths except "flipped." It is still a valid solution mathematically and needs to be accounted for. We can avoid such cases by utilizing more constraints, such as limiting the degrees at which each joint can turn.
More Complex Types
This 2D, double-jointed example is a very simple introduction to Inverse Kinematics. There are many more examples out there, such as utilizing 3 or more joints (which can be solved through linear algebra and trigonometry in a similar fashion) or even segments that can extend (which would require an optimization model to be utilized on your project). It must be noted that not all joints are bidirectional and that most are omnidirectional ball joints that can act in 3D space, which can move in any direction and add a new layer of complexity.
Programs have adapted to this, and often utilize a machine learning algorithm in order to accurately define each parameter. This leads to another path of optimization and modeling.
In optimization, a certain goal is defined. Constraints are given in the form of formulas and constants, and independent variables are defined for the model to change. Additionally, these models utilize a "point" system in order to achieve the most desirable result, which is often based on errors or parameters that the user sets. The model would then tweak the independent variables, with respect to the formulas and constants, to achieve the lowest error possible, trying each combination and earning "points" as it gets closer to the user's assigned goals. It's important to be able to create and define each of these parts for the optimization model in order to have efficient robotic motion.
Overall, inverse kinematics serves as the backbone for robotic movement. It's important to understand if you wish to utilize joints in your projects, and an invaluable tool for anybody incorporating machine learning into their robots. Although the math gets more complicated with each joint and segment, the possibilities remain endless.
Have questions or comments? Continue the conversation on TechForum, DigiKey's online community and technical resource.
Visit TechForum
