What Is RMS?

2024-11-18 | By Olivia West

Using the RMS, or root mean square, of a signal is essential to making calculations when dealing with fluctuating signals. To accurately predict and understand the behavior of your circuit, it is extremely important to know how and when to use RMS values.

What is an RMS value?

Any value indicated as RMS, usually labeled with subscript ‘rms’, is simply the root of the mean of the squared values measured over a period; they may also be taken over a specified length of time for a non-periodic signal. RMS values are often called effective values because they are the values in AC that will produce the same results in an equivalent DC circuit.

The RMS for any function y which exists over a period t=a to t=b is as follows:

What Is RMS?

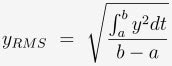
When you are solving for an average term that is dependent on a squared variable, you must use the RMS of the squared term.

Why do we use RMS?

Let’s take a closer look at the power equation, one of the principal applications of RMS, to see why this would matter.

What Is RMS?

Using these two equations, we can substitute IR for V and make a new equation.

What Is RMS?

You may note that the above equation is specific to an instantaneous reading. For a DC circuit, this works fine as current, and voltage are stable over time. However, in a circuit with alternating values, we cannot simply define the measure of current or voltage as a single quantity. So, we must modify the equation slightly to represent each of the variables accurately as a function of time.

What Is RMS?

Now, while instantaneous power or power as a function of time can be meaningful in some cases, we often want to find average power in an AC circuit. If we simply plugged in the average value of the alternating current or voltage, our result would be zero, since the current and voltage are just as often positive as they are negative (in one direction vs opposite). Using the original electric power equation, P=I×V, we would always get a positive answer as voltage has the same sign as current at any given instant. The following graphs help to visualize this relationship:

What Is RMS?

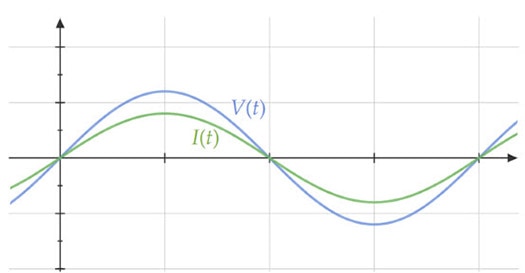
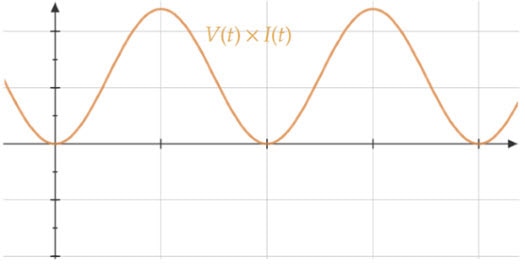
Because the RMS involves squaring the function before taking the average, the result is a positive value that, when squared, equals the average of the squared function. If you simply took the average of the absolute value of the function, the average would not account for the weighting that higher squared values have on the mean. This is why when using the squares of alternating waves, as in power equations dependent on resistance, you must use their RMS values instead of using their peak or mean. In practice, using the RMS value for a current or voltage that varies over time allows us to calculate the same average power as a constant current or voltage would produce with a given resistance.

Calculating RMS

Luckily, the RMS of some common waveforms are easy to calculate based on their peak or peak-to-peak values. For reference, here are three common waveforms and their rms values:

What Is RMS?

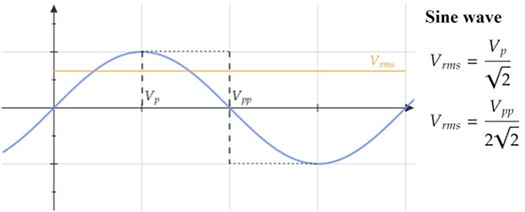
Note: These equations also apply when current is substituted for voltage.

However, if you are dealing with a signal that follows a different periodic waveform, you could use the integral calculation given earlier. Modern digital oscilloscopes can determine RMS values for complex or non-periodic waveforms, so calculation is not typically necessary, though it is important to note which value you are reading. If you are using an AC voltmeter or ammeter, it will usually display the RMS value of the voltage or current by default, and any peak readings will be explicitly labeled as peak. This has become standard because it is much easier to perform calculations when given the RMS value. Beware that the bandwidths of digital multimeters vary, so you may get erroneous readings depending on the bandwidth of your signal of interest.

When to use RMS values (and when NOT to)

Now that we know what RMS is and how to calculate it, it is important to note when it is appropriate to use RMS values in calculations. You will want to use an RMS value any time you are solving for a mean that depends on a square of that value.

A common application of needing an RMS value is measuring power dissipation through a resistor in an alternating circuit. In this case, the resistance is constant and either the voltage drop across the resistor or the current flowing through the resistor will be measured. In either case, the power varies with the square of the alternating signal, and the RMS value must be used. The power dissipation is equal to the square of the RMS voltage, divided by resistance, or the square of the RMS current, times the resistance.

There are also many occasions in which an RMS value should not be used. One example is in determining the average power consumed by an electronics unit powered by a power supply in which the input voltage is constant, and the input current varies with time. In this case, the input power is equal to the input voltage times the input current, P=I×V. Since neither of these terms are squared and the input voltage is constant, the average input current must be used to calculate the average input power.

Conclusion

While we have reviewed RMS in relation to the electric power equation, there are a vast number of applications of RMS inside and outside of the electronics world. From calculating the Poynting vector for measuring energy flow to calculating the molecular speed for effusion rates, understanding the purpose and necessity of RMS values is crucial to successful engineering design, measurement, and evaluation.