What is the Nyquist Theorem and Why is it Important
2024-12-02 | By Mustahsin Zarif
We have analog signals all around us: light waves, sound waves, and voltages. However, in order to make sense of this information and process it on a computer, we need to convert the analog signals into digital signals. This is done by sampling the continuous time (CT) signals to generate discrete time (DT) signals, and in order to accurately represent the signal in discrete time, we need to sample it at the Nyquist frequency. What is the Nyquist theorem that dictates this sampling frequency? Let's take a look at it.
Assume we have an analog signal which is a cosine wave with a frequency of 1 Hz and an amplitude of 1 unit.
In order to make sense of this real-world wave and process it on a computer or microcontroller which are discrete devices, we need to sample the CT wave using an impulse train to make a DT wave.
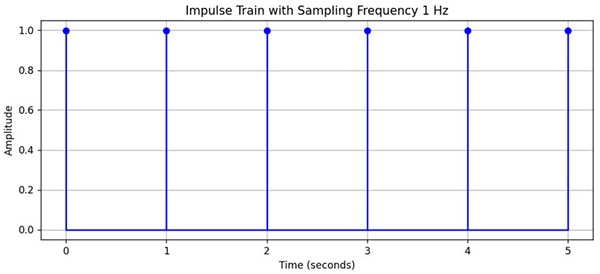
Now this impulse train can be given different frequencies to sample the analog signal at different rates. We multiply the analog signal by the impulse train to generate the discrete-time signal, but how do we go about choosing this ideal sampling frequency?
Let’s take an impulse train with a sampling frequency fs = 1 Hz (same as the frequency of the original wave). The sampled DT wave looks like the red line:
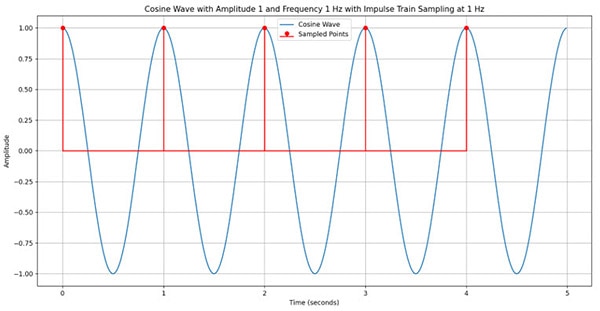
If we were to try to connect the red dots, we would get a straight line that does not resemble the cosine wave at all. Therefore, this is a poor choice of fs.
Now, take fs to be 10 Hz, 4 Hz, and 3 Hz, respectively.


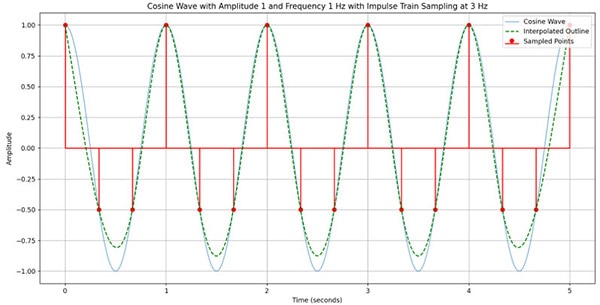
We can see that the higher the frequency, the better we can reconstruct the original cosine wave by estimating the way the dots connect. So, what is the minimum fs required for the DT signal to resemble the CT signal?
The Nyquist-Shannon sampling theorem states that a CT signal should be sampled at a rate greater than twice the maximum component frequency (wM) present in the signal. This is the Nyquist rate, and it prevents aliasing (more on this later). This allows signal x(t) to be recovered from its samples.
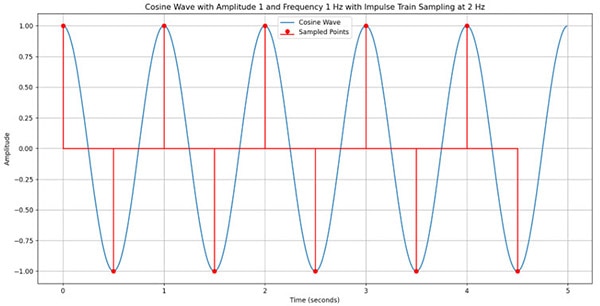
As we can see, we can estimate the shape of the original cosine wave with the stem plot at 2 Hz.
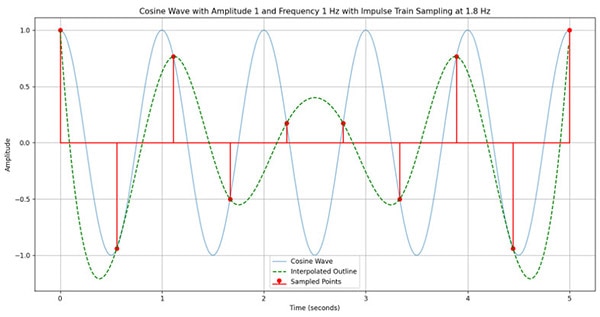
However, when fs = 1.8 Hz< 2 Hz, the stem plot cannot trace the original wave anymore. Therefore, this proves the Nyquist Theorem by trial and error.
Understanding why Nyquist Theorem works: a look into the Fourier domain
Every signal in the time domain can be represented in the frequency domain.
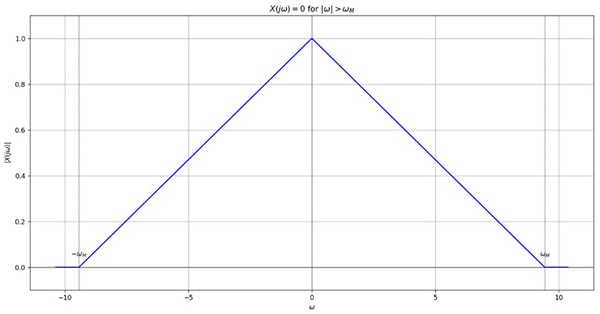
Look at a sinc2 function for example.
In the time domain:

In the Fourier domain:
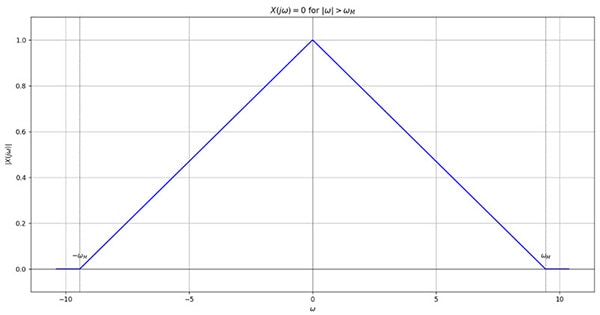
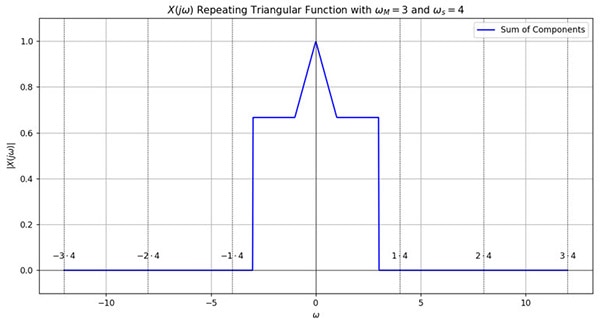
Now when we sample this wave, it creates copies of the triangle in the Fourier domain. A good sampling rate would ensure well-separated triangles, while a poor sampling rate would result in aliasing: copies of sampled signals overlapping in the frequency domain.
Therefore, a sampling rate of at least the Nyquist rate would result in the following graphs:

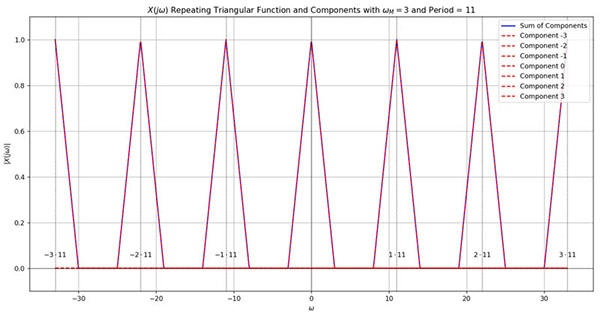
By applying a low pass filter that selects frequencies of less than or equal to the maximum known frequency of the CT wave, we can get the original triangle back.
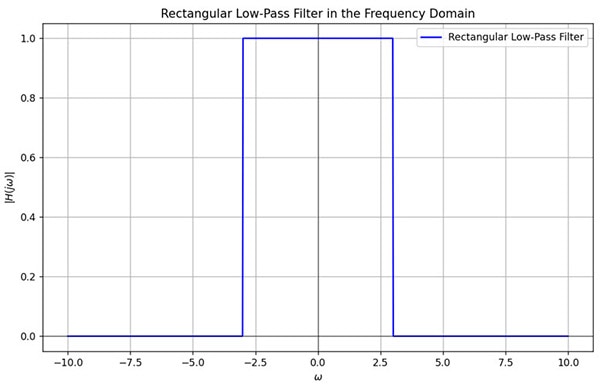
Multiplying the copies with this wave gives us the following wave:
In the time domain, this corresponds to the original sinc2wave!
So, what happens when we choose fs < Nyquist Rate for sampling on a computer? Well, taking ws = 2*pi*fs = 4 rad/s, we first get copies that result in the following shape:

If we apply the same low pass filter as before, we get the following graph:
This is not the Fourier transform of the original wave! As such, converting to the time domain would give us a CT signal that is different from the expected wave.
The process of reconstructing a CT signal can be summarized using a block diagram made using DigiKey’s Scheme-it tool. In conclusion, for us to work with real world signals in the digital world, we have to make sure that no information is lost during the analog-to-digital conversion. One way to do this is to sample the analog signal at a minimum of twice the maximum frequency of the wave, as stated by the Nyquist Theorem. As long as we abide by this theorem, our reconstructed x'(t) signal will be the same as the original x(t) signal.
Have questions or comments? Continue the conversation on TechForum, DigiKey's online community and technical resource.
















