Analog Computing: Solving Differential Equations

2024-02-07 | By Antonio Velasco

Previously, I talked about what analog computing is and how it works. This blog will serve as an example of utilizing Analog Computing and how it all works. Here, we'll go a bit more hands-on and utilize it to solve a differential equation related to a spring-mass system. We'll explore how to manipulate parameters, such as mass and spring constant, with potentiometers and variable capacitors, and read the output through a multimeter or oscilloscope.

The Setup

Imagine a spring-mass system—an object attached to a spring, oscillating back and forth. The motion of this system can be described by a second-order differential equation, which relates the displacement of the mass to time.

The equation for the oscillating spring-mass system is as follows:

Analog Computing: Solving Differential Equations

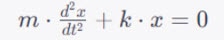
Where:

- m is the mass of the object.

- k is the spring constant.

- x is the displacement of the mass from its equilibrium position.

- Analog Computing: Solving Differential Equations represents the second derivative of x with respect to time, indicating the acceleration.

This differential equation depicts the motion of the system, and we can utilize analog computing to create a solver for it.

How to Utilize Analog Computing in This Scenario

To build your analog computer for solving this differential equation, you'll need a few essential components:

Spring: A physical spring that represents the spring constant k of the system. You can use springs with adjustable stiffness for variable parameters.
Mass: A weight that represents the mass m of the system. This weight is attached to the spring.
Potentiometers or Variable Capacitors: These components will allow you to adjust the values of m and k easily. Connect them in series with the spring and mass to vary the parameters.
Position Sensor: To measure the displacement x of the mass, use a potentiometer or a variable capacitor. This sensor converts the position into an electrical signal.
Signal Generator: Provide an input signal that represents the acceleration to drive the system. A simple function generator will work for this purpose.
Multimeter or Oscilloscope: You'll need a way to read the output signal, which represents the displacement x of the mass. A multimeter or an oscilloscope is ideal for this task.

Now, let's walk through the process of solving the differential equation for the oscillating spring-mass system using your analog computer:

Attach the mass to the spring and secure it.
Connect the potentiometers or variable capacitors in series with the spring and mass. These components allow you to adjust the values of m and k conveniently.
Connect the position sensor (potentiometer or variable capacitor) to measure the displacement x of the mass.
Connect the signal generator to provide an input signal representing the acceleration to drive the system.

Step 2: Parameter Adjustment

Begin with known values of m and k or set them to arbitrary values.
Use the potentiometers or variable capacitors to adjust the parameters, mimicking changes in mass and spring constant.

Step 3: Input Signal Generation

Configure the signal generator to produce the desired input signal representing the acceleration.
The choice of input signal depends on your specific problem. For simple harmonic motion, a sinusoidal signal works well.

Step 4: Measurement and Analysis

Monitor the output signal from the position sensor. This signal represents the displacement x of the mass.
Record and analyze the output signal using a multimeter or oscilloscope.
Observe the behavior of the system, including its amplitude and frequency, as you adjust the parameters.

Step 5: Parameter Optimization

Fine-tune the values of m and k to achieve the desired behavior or solution.
Experiment with different input signals to explore various scenarios.

Step 6: Interpretation

Translate the observed output signal into the physical context of the spring-mass system.
Understand how changes in m and k affect the system's response.

Wrapping It Up

Essentially, what analog computing here does is allow us to translate a physical system into one that utilizes pure analog computing. It provides an intuitive and hands-on approach to understanding the behavior of systems governed by complex mathematical equations. By manipulating physical components and observing their responses, you gain valuable insight into how parameters impact the system's behavior.

Analog computing is not just a theoretical concept—it's a tangible, hands-on adventure in computation. By constructing a simple analog computer using a spring-mass system and variable components, you can directly engage with the mathematics of differential equations. Through parameter adjustments and signal manipulation, you'll witness the real-world implications of changing m and k in your system. This hands-on approach fosters a deeper understanding of mathematical modeling and system dynamics.

To learn more about what Analog Computing is, check out my previous blog!