How To Simulate a PID Controller in Python for a DC Motor

2024-11-11 | By Jake Hertz

Controlling a DC motor's speed precisely requires feedback from the motor and a control algorithm capable of adjusting the motor's input based on desired performance. The Proportional-Integral-Derivative (PID) controller is one of the most widely used methods for achieving this.

In this tutorial, we'll simulate a simple PID controller for a DC motor in Python without using classes. The controller will aim to adjust the motor's speed based on feedback from an encoder, with the PID loop handling the control logic.

PID Overview

In this project, we will implement a PID controller that adjusts the PWM signal to the motor based on the speed feedback provided by the encoder. To do this, the following components are needed.

Overview of the PID Controller

The PID controller adjusts the motor speed using three components:

Proportional (P): Reacts to the current speed error (difference between desired and actual speed).
Integral (I): Accounts for the accumulation of past errors.
Derivative (D): Predicts future errors based on the current rate of change.

How To Simulate a PID Controller in Python for a DC Motor Figure 1: Block diagram of a PID control system.

The formula for PID control is as follows:

How To Simulate a PID Controller in Python for a DC Motor

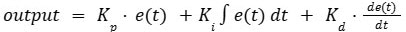
Where:

K_p, K_i, and K_d are the tuning parameters for the proportional, integral, and derivative terms.
e(t) is the error (difference between the setpoint and the current speed).

Motor Simulation Overview

The motor model used in this simulation significantly simplifies a real DC motor's behavior. In this model, we assume a direct linear relationship between the control signal and the motor speed, overlooking various complexities present in actual systems. Real motors exhibit friction, inertia, and non-linear responses, which are not accounted for in this simulation. Factors such as motor inductance, back EMF, and torque-speed relationships are omitted, reducing the model’s accuracy.

In a real-world scenario, the motor's response would lag due to physical constraints, and it might not react instantaneously to control inputs. External factors like load changes and power supply variations could also affect performance. While useful for understanding the fundamentals of PID control, this simplified approach is idealized and should be expanded upon for real-world applications by incorporating more detailed models that consider these physical attributes.

Code Implementation

1. Imports and Simulation Parameters

Copy Code

import matplotlib.pyplot as plt
import numpy as np

We first import the necessary libraries. matplotlib.pyplot is used for plotting the motor speed over time, and numpy is used for generating an array of time steps to simulate the passage of time.

Copy Code

setpoint = 100  # Desired motor speed (RPM)
Kp = 0.1        # Proportional gain
Ki = 0.01       # Integral gain
Kd = 0.05       # Derivative gain
dt = 0.1        # Time step for simulation (seconds)
sim_time = 150   # Total simulation time (seconds)

This section initializes key parameters for the simulation:

setpoint: The desired motor speed in RPM.
Kp, Ki, and Kd: The proportional, integral, and derivative gains for the PID controller. These are tuning parameters that affect how the controller responds to errors.
dt: The time step for each iteration in the simulation. This is how frequently the PID loop updates.
sim_time: The total duration for which we will run the simulation, in seconds.

2. PID Controller Initialization

Copy Code

integral = 0
previous_error = 0

motor_speed = 0  # Initial motor speed (RPM)

# Store data for plotting
time_data = []
speed_data = []

integral = 0
previous_error = 0

motor_speed = 0  # Initial motor speed (RPM)

# Store data for plotting
time_data = []
speed_data = []

integral: The integral term accumulates the error over time. We initialize it to 0.
previous_error: This tracks the error from the previous time step to compute the derivative term.
motor_speed: The motor’s speed is initially set to 0 RPM (the motor starts from rest).
time_data and speed_data: These lists store the simulation’s time steps and corresponding motor speeds. They will be used later for plotting.

3. Main PID Loop

Copy Code

for t in np.arange(0, sim_time, dt):
    # Calculate error between setpoint and current motor speed
    error = setpoint - motor_speed

This loop runs for each time step in the simulation. The np.arange(0, sim_time, dt) generates a list of time steps from 0 to sim_time with a step size of dt.

error: The error is the difference between the desired speed (setpoint) and the current motor speed.

4. Proportional, Integral, and Derivative Terms

Copy Code

# Proportional term
    P_out = Kp * error
    
    # Integral term (accumulation of past errors)
    integral += error * dt
    I_out = Ki * integral
    
    # Derivative term (rate of change of error)
    derivative = (error - previous_error) / dt
    D_out = Kd * derivative

Proportional term (P_out): This term is the product of the proportional gain Kp and the error. It gives an immediate reaction based on the current error.
Integral term (I_out): The integral of the error is accumulated over time to counter persistent, small errors. This is calculated by multiplying the accumulated error (integral) by the integral gain Ki. The error is multiplied by dt before accumulating, ensuring it scales appropriately with time.
Derivative term (D_out): The derivative term reacts to the rate of change of the error, helping to dampen the system's response. It’s computed by taking the difference between the current and previous error, divided by dt (the change in time).

5. Control Output and Motor Simulation

Copy Code

 # Calculate the total control output
    control_output = P_out + I_out + D_out
    
    # Simulate the motor speed response (simplified linear response)
    motor_speed += control_output * dt

control_output: The total control signal is the sum of the proportional, integral, and derivative outputs. This is the input to the motor to adjust its speed.
motor_speed: The motor speed is updated based on the control output. In this simplified model, we assume the motor speed changes linearly with the control output over time (using dt to adjust for time steps). In a real system, this would be much more complex, considering factors like inertia, friction, and electrical dynamics.

6. Updating Error and Storing Data

Copy Code

# Update the previous error for the next iteration
    previous_error = error
    
    # Save data for plotting
    time_data.append(t)
    speed_data.append(motor_speed)

previous_error: The current error is stored for use in the next iteration, as it will be needed to compute the derivative term in the next time step.
time_data.append(t) and speed_data.append(motor_speed): The current time and motor speed are appended to their respective lists, which will be used to plot the motor speed over time at the end of the simulation.

7. Plotting the Results

Copy Code

# Plot the motor speed over time
plt.plot(time_data, speed_data)
plt.title('DC Motor Speed with PID Control')
plt.xlabel('Time (s)')
plt.ylabel('Speed (RPM)')
plt.grid(True)
plt.show()

After the simulation loop finishes, we use matplotlib to plot the motor speed over time.

plt.plot(time_data, speed_data): This creates a line graph of the motor speed (speed_data) versus time (time_data).
plt.title(), plt.xlabel(), plt.ylabel(), and plt.grid() are used to add labels and a grid to the plot, making it easier to read.

Finally, plt.show() displays the plot.

Interpreting Results

The result, shown in Figure 1, depicts the DC motor speed over time under PID control, as implemented in the code. The motor speed rapidly increases at first, peaking at around 120 RPM, which represents the overshoot caused by the high initial error between the setpoint (100 RPM) and the motor's starting speed (0 RPM). This overshoot occurs due to the combined effect of the proportional and integral terms in the controller.

How To Simulate a PID Controller in Python for a DC Motor Figure 2: The DC motor speed over time under PID control.

After the peak, the speed decreases as the error reduces, and the derivative term dampens the response, leading to an undershoot below the setpoint. The system then oscillates slightly before settling at the desired speed of 100 RPM, reflecting the PID controller's attempt to correct the error dynamically.

The overshoot, undershoot, and gradual settling behavior are typical of PID-controlled systems. The motor eventually stabilizes near the setpoint due to the combined action of all three PID terms, with some fine-tuning likely needed for quicker convergence.

Tuning the PID Controller

The performance of a PID controller heavily depends on how you tune the gains (Kp, Ki, Kd). Here’s a general guideline:

Increase Kp to make the system more responsive but watch for overshoot.
Increase Ki to eliminate steady-state error but be careful with integral windup, which can cause instability.
Increase Kd to smooth the response by reducing oscillations, though too much can cause a slow response.

Conclusion

In this tutorial, we simulated a simple PID controller for a DC motor in Python. We used basic mathematical models to simulate the motor's speed and showed how a PID controller can bring the system to a desired speed. This example is a great starting point for more complex control systems or tuning experiments in real-world applications.

To extend this simulation: