设置
快速交货
免运费
国际贸易术语
支付类型
市场产品
制造商零件编号 CFR-25JB-52-3K3
RES 3.3K OHM 5% 1/4W AXIAL
YAGEO
The Basics of Low and High-Pass Filters
2024-11-11 | By Aiden Warne
Breadboards Capacitors Resistors
Introduction To Low and High-Pass Filters
Low and high-pass filters are used widely in the electrical engineering world. For example, these low and high-pass filters can be used in audio processing, image processing, communication systems, and sometimes biomedical signal processing. These filters do as their name suggests. They can filter out either a high frequency and let low frequencies pass, and they can do the opposite, filter out low frequencies and let high frequencies pass. In this blog, I am going to find the waveforms of the given high-pass and low-pass filter circuits for the components I am using. Upon building the circuit, I am going to compare the waveforms of the signal from the frequency to the waveform from the circuit components and see if they are the same or out of phase. I am going to use a function generator as well as an oscilloscope to measure these waveforms.
What Are Low and High-Pass Filters?
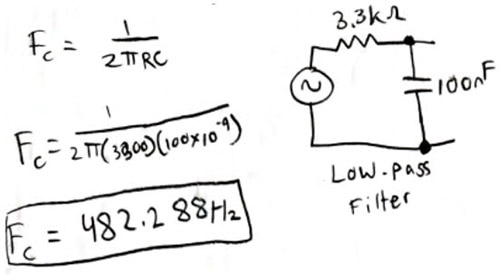
Low and high-pass filters, as discussed before, either filter out frequencies lower than the cut-off frequency or higher than the cut-off frequency. This cut-off frequency is determined by the equation listed below, where R is the resistance of the resistor, C is the capacitance of the capacitor, and 2π is a constant. This cut-off frequency and the order of the components determine how the circuit will respond to a given input frequency. A low-pass filter has the resistor first and then the capacitor second. Rather, the high-pass filter has the capacitor and then the resistor. If the input frequency is greater than the cut-off frequency and it is a high-pass filter, then the waveform will pass through unfiltered. If the input frequency is less than the cut-off frequency, then the waveform will be filtered and be out of phase and have a lower amplitude compared to the input waveform. The opposite is true when it comes to low-pass filters.
How To Calculate Frequency Cut-Off
As stated above, the cut-off frequency is the frequency in which the low or high-pass filter filters out the frequency, which is calculated in the equation: 12RC. As stated above, R is the resistance of your component and C is the capacitance of your component. All that is needed for a high-pass filter is one capacitor, one resistor, and of course some jumper wires and a power supply. For this project, I used a 3.3k resistor and a 100 nano farad capacitor. For low and high-pass filters, you can really use any component values you want to. I used these specific components for ease of use and to get nicer values for a cut-off frequency. As shown below, I put my values in the given equation and came up with a cut-off frequency of 482.288Hz. This is the frequency in which the circuit will balance between to make the high and low-pass filters.
You can also use DigiKey’s Low Pass/High Pass Filter Calculator to find these values.
Hand Calculations
Simulations
Multisim Low-Pass Circuit
Here, I used a circuit simulation software called Multisim. With this, I was able to confirm my hand calculations by seeing that the higher frequency was indeed cut off after it reached the cut-off frequency of 482.288Hz. The graph shows that the amplitude is high in the lower frequency region, but as it crosses 482Hz, it starts to taper off and go in a negative direction. With the resistor first in order, in series with the capacitor, this creates the low-pass filter. The power source that is connected to it is a function generator, giving off a pulse that allows the waves to be seen on the oscilloscope. You can also do this with the high pass filter.
Physical Circuit Build
Low-Pass 10Hz 3.3k Ohms 100nF
In the picture above, the low-pass filter circuit is built on the breadboard. The waveform is applied first through the resistor and then through the capacitor. The input frequency applied is less than the cut-off frequency, thus the filtered waveform is in phase and has no difference in amplitude compared to the input waveform. According to my understanding of low-pass filters and comparing this to my hand calculations, this makes sense.
Low-Pass 1kHz 3.3k Ohms 100nF
Again, the low-pass filter circuit is pictured above. This time, the input frequency applied is more than the cut-off frequency, thus the filtered waveform isn't in phase and there is a difference in amplitude compared to the input waveform. For reference, the blue waveform (the applied waveform) is at 2 volts per division and the yellow waveform (the filtered signal) is at 1 volt per division. According to my understanding of low-pass filters and comparing this to my hand calculations, this makes sense.
High-Pass 4.4kHz 3.3k Ohms 100nF
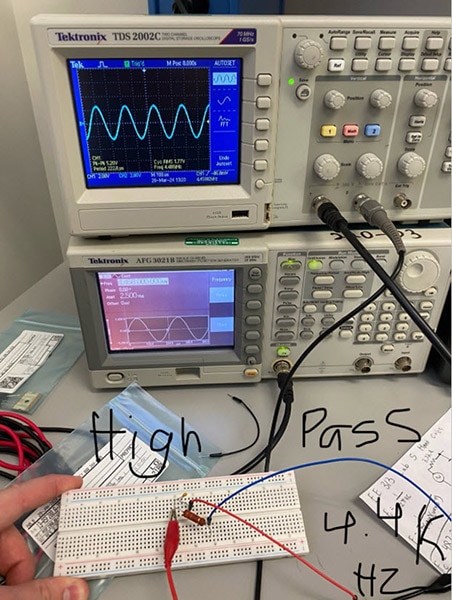
In the picture above, the high-pass filter circuit is built on the breadboard. The waveform is applied first through the capacitor and then through the resistor. This is the opposite of the low-pass filter. The input frequency is more than the cut-off frequency; thus, it will be in phase and has no difference in amplitude compared to the input waveform. According to my understanding of high-pass filters and comparing this to my hand calculations, this makes sense.
High-Pass 10Hz 3.3k Ohms 100nF
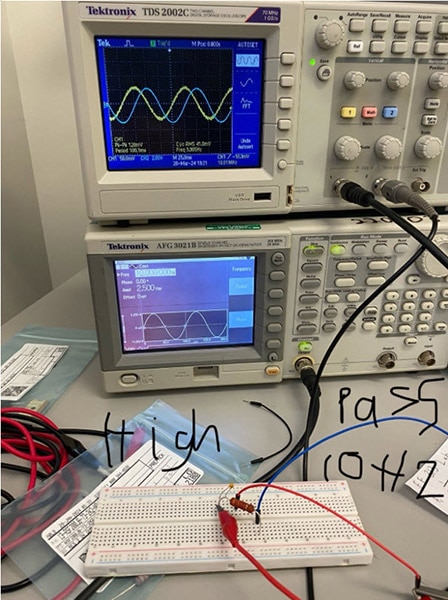
Again, the high-pass filter circuit is pictured above. This time the input frequency applied is less than the cut-off frequency, thus the filtered waveform isn't in phase and there is a difference in amplitude compared to the input waveform. For reference, the blue waveform (the applied waveform) is at 2 volts per division and the yellow waveform (the filtered signal) is at 50 millivolts per division. According to my understanding of low-pass filters and comparing this to my hand calculations, this makes sense.
Results
When doing the simulation and real experiments, I got very similar waveforms and they compared and matched what they should be. The low-pass filter, in which the cut-off was 482 Hz, allowed a 10 Hz frequency to go through, but not a 1K Hz to go through, which is what I was expecting. The high-pass filter had the expected outcome as well, with the high frequency waves lining up, and the lower ones not getting passed through.
Conclusion
In conclusion, I was able to get a better understanding of how low-pass and high-pass filters work, as well as how the frequency cut-off works with the given components. I was also able to clearly see the similarities and differences between the waveforms when the components were flipped around. You can make a high or low-pass filter with any combination of resistor and capacitor and can figure out the cut-off frequency the circuit will have using the equation I have provided. This can be a fun little project anyone can do with a few supplies and is a good little learning experience to anyone wanting to know more about frequencies in electronics.
Have questions or comments? Continue the conversation on TechForum, DigiKey's online community and technical resource.
Visit TechForum
