Audio Coding and Compression for Microcontrollers
投稿人:DigiKey 欧洲编辑
2011-12-07
Adding speech and sound generation to a product can greatly improve the usability and marketability of a product and it does not demand the addition of a separate digital signal processor (DSP) or specialized audio processor to implement. Microcontroller (MCU) vendors have implemented DSP extensions that bring real-time decoding for algorithms once thought too complex to implement on anything but a dedicated DSP platform.
Furthermore, audio processing provides a large number of tradeoffs that can be exploited by designers to allow sophisticated audio to be played on comparatively low-speed 8-bit MCUs. For example, it is possible to implement simple versions of the standard Adaptive Differential Pulse Code Modulation (ADPCM) algorithm on a relatively simple MCU, such as a Microchip Technology PIC16 without demanding any DSP extensions.
Audio-coding techniques designed to reduce storage size fall into two categories. The first method is called waveform coding, which uses the known properties of the waveform itself. The advantage of waveform coding is that it attempts to code signals without any knowledge about how the signal was created. This allows the codec to be applied to different forms of audio even though the algorithm may have been designed for, say, speech.
Speech-oriented waveform codecs often take advantage of the observation that there is a higher probability of a speech signal taking a small value rather than a large value. Therefore, a speech processor can reduce the bit rate by quantizing the smaller samples with finer step sizes and the large samples with coarse step sizes. The bit rate can further be reduced by using one inherent characteristic of speech: a high correlation between consecutive speech samples.
Rather than encode the speech signal itself, the difference between consecutive samples can be encoded. This method is a relatively simple one that is repeated on each sample with little overhead from one sample to the next. ADPCM is an example of a waveform algorithm that uses this technique.
The other form of compression or coding is to use a model of the way that the audio signal is created. This can dramatically improve compression ratios without negatively affecting the quality of the audio once reconstructed. For example, the speech codecs used commonly for cellular telephony networks use a simplified model of the vocal tract.
Speech typically remains relatively constant over short intervals and a set of parameters can be used to define how a short period of speech can be reconstructed: typically pitch and amplitude. These parameters rather than coded samples can then be stored or transferred to the receiver. This technique requires significant processing on the incoming speech signal as well as memory to store and analyze the speech interval. Examples of this type of processor, called a vocoder or hybrid coder, are those which perform linear predictive coding (LPC) or code-excited linear predictive coding (CELP).
The GSM telephony standard uses CELP to compress real-time speech to a stream that needs a bandwidth of less than 10 kb/s. For non-telephony uses, the Speex codec provides an efficient implementation of a CELP algorithm and is available as open-source code. A number of libraries for MCUs, such as the one developed by Microchip Technology for the PIC32MX family, implement the Speex codec.
The MPEG2 Layer 3 (MP3) audio codec uses a model of the human hearing rather than vocal system to determine how best to compress an audio stream. Many of today’s leading audio codecs are lossy, perceptual codecs that work on the basis that the brain cannot hear certain audio signals that are ‘masked’ by other, louder signals. Therefore, they are not worth encoding, making it easier to render the audio with a lower bitrate stream of data.
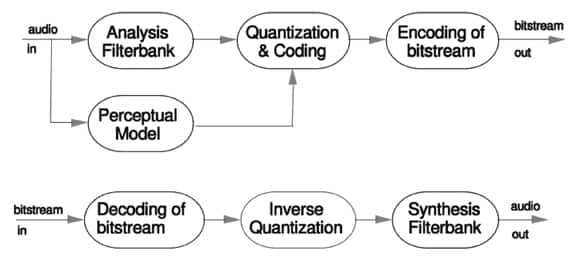
Figure 1: Block diagram of a perceptual codec. (Source: Fraunhofer)
Other high-quality audio codecs use a waveform-formed approach and these are typically lossless algorithms, such as Free Lossless Audio Codec (FLAC), which were developed in response to the problems that algorithms developed for generic data streams have with audio data. Most conventional text-oriented data-compression techniques, such as ZIP and GZip, rely on the understanding that there is a high level of redundancy in textual information but little correlation between the data values in the stream. The compressor builds a dictionary of commonly used characters of data that are then identified using a much shorter sequence of bits. For example, a space character may take three bits; an ‘x’ five or six and rarely used symbols more than eight bits. This lies at the core of Huffman encoding. However, its compression factor is not as good as that used in common PC-based software such as ZIP.
For example, an improvement on Huffman encoding used in text-file compressors is the LZW algorithm which moves beyond individual symbols to short sequences – for example ‘anti’ is more common in text than ‘atni.’ Similarly, some machine code instructions and address ranges are far more common in software than others. Those sequences that repeat often are given the shortest symbol in the dictionary that the compressor builds. The encoded versions of very rare sequences can become longer than their counterparts in the source.
In audio, the individual samples are often strongly correlated with each other but sequences do not repeat exactly. As we have seen with ADPCM, successive samples are frequently similar in value but, crucially, they are not identical. This disrupts the ability of a compression system designed for text or machine code to efficiently encode the sample stream. The FLAC algorithm works around this problem by using linear prediction, similar to that employed by ADPCM, as the first stage in encoding the sample data. This leaves a series of uncorrelated values – called the residual or error signal – that can be entropy coded. Rather than Huffman encoding, FLAC uses the Golomb-Rice method – this family of codes is suited to situations where small values are more likely to be present than large values.
In general, Golomb codes use a tunable parameter, M, to divide the value into two parts. The first is a division by M; the second is the remainder. The first part is stored as a unary code – one where the number, n, is represented by n-1 ‘0’ digits followed by a terminating ‘1’ or vice versa. This allows smaller values to be packed more densely. The Rice variants of this coding scheme makes M a multiple of two to improve efficiency on microprocessors – the divisions, for example, can be implemented as simple shift operations. The remainder is encoded using truncated binary encoding, another scheme optimized for small residuals.
For embedded systems, MP34 will be the scheme most commonly encountered when high-quality audio is desired but storage space is at a premium. The core of the system is the perceptual model, which was based on years of research into the way that the brain processes audio information. In general, loud sounds of one frequency will mask quiet sounds of frequencies that are close by. They are not necessarily completely masked, but it means that the frequency bands with the quiet signals can be coded at a lower level of resolution with more bits allocated to the frequency band with the louder signal.
The first stage, therefore, is to split the incoming time-domain signal into a group of narrow frequency ranges using a filterbank. This is then analyzed to determine the masking threshold for each band and, with that, the allowed level of noise for that band. The allowed level of noise will determine how few bits can be applied to that band – the fewer the bits, the larger the amount of quantization noise that will be generated when the audio is reconstructed.
The audio itself is processed using a modified discrete cosine transform (MDCT) to convert the time-domain signal into frequency-domain information. Using the information from the perceptual model, the algorithm can then proceed with quantization. The technique chosen was a power-law quantizer, which codes larger values with lower resolution. This performs a level of noise shaping, improving accuracy with smaller signals.
The quantized levels are then encoded using Huffman codes – this part of the algorithm is lossless, as with other data compression that use Huffman coding. Even after power-law quantization and Huffman coding, the output data stream will probably be at a higher rate than has been set for the coder. Increasing levels of quantization are needed to generate streams that fit within a 128 kbit/s, 96 kbit/s or other typical setting for MP3.
To provide the required output rate, the quantizer is normally implemented using two nested iterative loops. The inner loop is the rate loop, modifying the overall coder rate until the output stream is at a low enough bitrate. This is achieved by applying larger quantization step sizes. The outer loop shapes the quantization noise using the masking thresholds that the perceptual model provided. Each change mandated by this outer loop demands a further pass through the inner loop to ensure that the output bitrate is below its threshold. The outer loop proceeds until the noise of each of the bands is below the masking threshold. Because of the number of iterations, it is very difficult to guarantee real-time operation for the encoding process.
Other, more sophisticated schemes have followed MP3, such as the Vorbis open-source codec5 developed for the Ogg format, and the AAC codec used in follow-ups to the MP3 standard. However, they use the same broad scheme but simply improve factors such as spectral resolution. For example, the MDCT algorithm used by AAC works with 1024 frequency lines rather than the 576 of MP3.
Because there is no need to run the perceptual model and the two rate-limiting loops, decoding from these lossy formats is much less compute-intensive than encoding – allowing implementation on a wide range of embedded processors. Furthermore, the designers of the MP3 standard worked to minimize the number of normative elements it contains. Only the data representation and decoder are treated as normative and, even then, the decoder is not specified in a bit-exact manner but in the form of formulas with a test available to check the implementation against one performed using double-precision arithmetic throughout. This makes it possible to implement decoders using fixed- or floating-point arithmetic. Fully compliant decoders have been written that use fixed-point words as short as 20 bits.
The MP3 decoder is well within the capabilities of a large number of 32-bit MCUs, such as those that employ the ARM7 or Cortex-M3 processor cores. Also, for popular architectures such as ARM, reference code is available that simplifies the implementation of MP3 as well as full source code for Vorbis and FLAC6 transcoders.
Researchers have, during the past 20 years, developed highly efficient ways of performing the most compute-intensive step – the DCT – using transformations to reduce the overall number of additions needed if a fast 32-bit multiplication instruction is not available. The Helix implementation, for example, when run on an ARM7 core, can support a sample rate of 44.1 kHz for a stereo output with a 128 kbit/s input stream at a clock rate of 26 MHz.
Where higher-performance DSP instructions are available, it is possible to optimize the audio processing, leaving more headroom for system functions. For example, the Cortex-M3 core used in the STMicroelectronics STM32 family of MCUs has a 32-bit multiply and accumulate instruction that is ideal for processing audio data. It also performs branch speculation to improve performance in loops that require branches. For example, a number of lookup table algorithms used to generate cosine values use a small number of branches.
The STM32F10x is accompanied by a DSP library that implements many of the functions used in audio processing in addition to transcoding. For example, the library includes routines for performing finite and infinite impulse response filtering commonly used to manipulate an audio stream and remove or enhance certain frequency bands. An FFT function can be used for real-time audio analysis.
Other architectures are also a good fit for audio compression and decompression algorithms. The Freescale ColdFire family of MCUs provides a cost-optimized solution for audio processing. Devices such as the MCF5249 implement an enhanced multiply-accumulate unit that is ideal for running audio filters and related algorithms and include I²S ports for communicating with ADCs and DACs. The MCF5249 is optimized for recording and playback systems as it includes direct interfaces to flash storage as well as IDE-based hard drives.
The Atmel AT32UC3A3 supports audio sample rates up to 50 kHz and adds to its already efficient instruction pipeline a set of DSP instructions. It can communicate with audio ADCs over the I²S bus and even includes its own bitstream DAC, making it an ideal platform for audio playback devices.
The DSP extensions include saturating arithmetic in which, instead of large values overflowing a register and forcing it to wraparound as conventional MCU arithmetic would, simply allows the value to reach a maximum. This provides a result that is more compatible with audio filters and avoids the need for branches in filtering loops to check for overflow, greatly increasing performance. The DSP extensions also add a variety of multiply instructions.
The Microchip PIC32MX is based on the MIPS RISC architecture, providing the core level of performance needed to handle FLAC, MP3 and other audio codecs. The company also supplies an audio library for a number of algorithms including ADPCM transcoding as well as Speex.
The Analog Devices ADSP-BF527 goes a step further in terms of signal-processing functions, providing a wide range of DSP instructions implemented with full MCU functionality to help realize advanced audio applications such as voice-over-IP phones where a range of advanced voice and audio codecs may be wanted and for multichannel audio input and output. There are up to twelve direct memory access (DMA) offload data transfer overhead from the processor core, allowing more headroom for DSP and control operations.
Audio is now a key part of many embedded systems and not just music players and speech recorders. The available codecs and coding techniques make it possible to optimize storage and playback for specific applications. The variety of audio-capable MCUs offered from distributors such as DigiKey provide the designer with the opportunity to choose a device that is ideally suited for the target system.
Summary
This article has provided an overview of the key audio compression and coding standards in use today and described a number of MCU architectures and implementations that are suitable for running a variety of them. Microcontrollers discussed include products from Analog Devices, Atmel, Freescale Semiconductor, Microchip Technology, and STMicroelectronics. You can obtain more information by utilizing the links provided to pages on the DigiKey website.
References:
- http://www-mobile.ecs.soton.ac.uk/speech_codecs/standards/adpcm.html.
- http://www.cprogramming.com/tutorial/computersciencetheory/huffman.html.
- http://www.inference.phy.cam.ac.uk/itprnn/code/c/compress/.
- MP3 and AAC Explained.
- http://www.vorbis.com.
- http://flac.sourceforge.net/.

免责声明:各个作者和/或论坛参与者在本网站发表的观点、看法和意见不代表 DigiKey 的观点、看法和意见,也不代表 DigiKey 官方政策。






 中国
中国