模拟基础知识 — 第 4 部分：优化三角积分 ADC 以实现低噪声

编者按：模数转换器 (ADC) 将模拟世界连接到数字世界，因此是连接到现实世界的任何电子系统的基本部件。它们也是决定系统性能的关键因素之一。本系列文章探讨 ADC 的基础知识、各种 ADC 类型及其应用。本系列中第 1 部分的模拟基础知识讨论了 SAR ADC。第 2 部分讨论三角积分转换器。第 3 部分探讨流水线 ADC。本文为第 4 部分，将说明三角积分 ADC 如何能够生成超低噪声结果。第 5 部分探讨 SAR ADC 难以处理的输入驱动问题。

三角积分 (ΔƩ) 集成电路拓扑仍在模数转换器 (ADC) 中广泛使用，为过程控制、精密温度测量和称重仪应用提供高分辨率、高集成度和低功耗的解决方案。

关于这种转换器有一个令人费解的事实，它从 1 位转换开始，理论信噪比 (SNR) 为 7.78 dB，相当于 5 V 系统中存在 2 V (V_RMS) 噪声。在此基础之上，该 ADC 可发展为真正的 24 位三角积分转换器，提供 146 dB 的理论 SNR，相当于 5 V 系统中存在 244 nV 的 RMS 噪声。

分辨率能够从 1 位跃升至 24 位，主要依赖过采样算法、噪声整形调制器和数字滤波器来降低量化噪声并提高 SNR。通过改用放大器输入级馈入 12 位或 16 位逐次逼近寄存器 (SAR) ADC，这种方法可以规避 ΔƩ 转换器的复杂性及其相关的噪声。此设计路径行之有效，但需要在印刷电路板上使用更多的集成电路并增加 BOM 成本。

有一种更好的方法可以解决噪声问题：利用超低噪声 ΔƩ ADC，该问题可以迎刃而解。

本文将简要讨论低噪声目标应用以及如何在内部设计 ΔƩ ADC 来满足这一要求。然后介绍 Texas Instruments 的两款 ΔƩ ADC，其中一款强调 24 位精度，另一款强调 32 位精度，同时还将说明如何利用这两款产品中强大的数字滤波功能。

适合 ΔƩ ADC 的应用场合

从模拟的角度来看，工程师在测量温度、压力、测压元件和光学传感器的输出时，需要不同的精度。从根本上讲，放大器增强了设计人员量化这类较小模拟量（多数情况下接近于 DC）的能力。渐进式数字化带来了视角和功能上的变化，同时增强了存储和修改传感器信号的能力。

为实现数字捕获，典型的传感器信号路径始于传感器，经过增益、多路复用和滤波器级，然后到达 ADC（图 1a）。

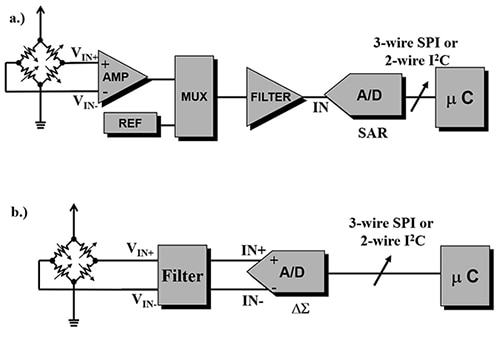图 1：使用 SAR ADC (a) 或 ΔƩ ADC (b) 将传感器信号数字化的两种技术。对于高分辨率电路，SAR ADC 需要放大功能和五阶有源滤波器，ΔƩ ADC 则需要前端模拟一阶无源滤波器。（图片来源：A Baker’s Dozen: Real Analog Solutions for Digital Designers，B. Baker，ISBN 0-7506-7819-4）

图 1a 中的转换器是一个 SAR ADC，可以执行 12 位到 18 位转换，并且能以高达 10 兆次采样/秒 (MSPS) 的转换速率运行。16 位转换器可提供 2¹⁶，即 65,536 个段。在 5 V 系统中，最低有效位 (LSB) 为 5 V/2¹⁶²⁹⁸，即 76.3 mV，理论 SNR 等于 98 dB。通过在 SAR 转换器之前执行模拟增益，可以实现更高的精细度。

ΔƩ 信号链（图 1b）利用单个转换器提高了信号链的分辨率，同时也降低了 BOM 成本。ΔƩ ADC 可提供 16 位到 32 位转换。在此信号链中，24 位 ΔƩ ADC 可提供 2²⁴，即 16,777,216 个段。因此，在 5 V 系统中，LSB 为 5 V/2²⁴，即 298 nV，理论 SNR 等于 146 dB。此分辨率水平为转换器提供了更加接近传感器能力的精细度。

由于内部数字滤波器需要时间来实现滤波计算，因此 24 位 ΔƩ ADC 的速度较慢。该转换器的典型输出数据速率范围为几赫兹至 1 MSPS。请注意，模拟滤波器现在采用的是便宜的一阶电阻电容 (RC) 滤波器，而不是复杂的三重运算放大器五阶模拟滤波器。

这两种方法的噪声之间区别很明显：ΔƩ ADC 的低噪声性能优于 SAR ADC（表 1）。

*备注：SNR = 6.02 N + 1.76，其中 N 是位数

表 1：16 位 SAR ADC 和 24 位 ΔƩ ADC 的 ADC 段数、LSB 和理论 SNR，满量程输入电压为 5 V。（数据来源：Digi-Key Electronics）

在温度、压力和测压元件这类传感器解决方案中，若不太注重速度规格，但精度至关重要，那么 ΔƩ ADC 可提供出色的解决方案。该 ADC 可通过使用数字而不是模拟降噪技术，实现低至上述小电压值的转换。

ΔƩ ADC 的内部构造

ΔƩ ADC 的内部 80% 为数字构造。通常，转换器接收输入信号，并立即将该模拟信号转换为数字信号。然后，转换器将该数字信号与后续的调制器转换合并到一个数字滤波器级，在该滤波器级中，累加的 1 位信号变为多位。接下来，转换器通过数字输出级，以串行方式将最终的多位转换发送到等待的微控制器。

模拟信号首先通过外部的一阶抗混叠滤波器 (AAF)。然后，噪声整形 (NS) 调制器获取模拟信号，并以转换器的时钟速率生成 1 位信号流进入数字滤波器（图 2）。

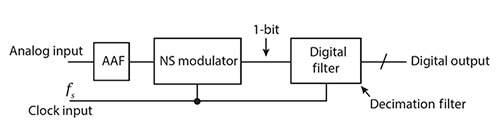图 2：典型 ΔƩ 使模拟信号通过一阶 AAF，使用 NS 调制器生成 1 位信号流，然后在连接到微控制器的数字输出端产生一个多位结果。（图片来源：CMOS: Mixed-Signal Circuit Design，2^nd Edition，J. Baker，ISBN 978-0-470-29026-2）

数字滤波器按时钟输入 1 位信号流中的多个代码，并在数字滤波器中创建完整的多位结果。这些多位结果将通过数字输出进行串行传输。

ΔƩ 调制器

积分器/反馈回路的数量决定了 ΔƩ 调制器的阶数。一阶 ΔƩ ADC 调制器只有一个积分器和反馈环路（图 3）。

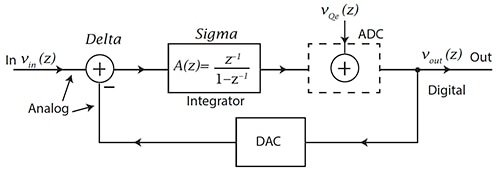图 3：一阶调制器具有一个模拟积分器以及 1 位 ADC 和反馈回路中的 DAC。V_Qe(z) 是量化 ADC 噪声。（图片来源：CMOS: Mixed-Signal Circuit Design，2^nd Edition，J. Baker，ISBN 978-0-470-29026-2）

在图 3 中，模拟信号 (V_IN(z)) 进入调制器的 Delta (Δ) 部分。然后，模拟信号经过积分器级或 Sigma (Ʃ) 级到达一个 1 位 ADC（根据图 2，采样率为 f_S），该 ADC 可以是比较器。现在，这一经过时钟数字化处理的信号反馈到 1 位数模转换器 (DAC)，同时继续前往 Δ 级的 V_OUT(z)。1 位 DAC 提供了一个需要从模拟输入信号 V_IN(z) 中扣减的模拟电压。该一阶调制器的传递函数为：

 公式 1

由于存在积分器和反馈回路，调制器在本身的数字输出数据流上实现了噪声整形算法（图 4）。

图 4：在位于 ΔƩ 调制器输出端的噪声整形函数中，噪声传递函数 (NTF) 等于 1-z^-1，其中 0.5 归一化频率等于 F_S/2。（图片来源：Understanding Delta-Sigma Data Converters, Schreier，Temes，ISBN 0-471-46585-2）

在图 4 中，噪声整形特性是降低转换 1 位量化噪声的第一步。随着噪声成功推至更高频率，由一个低通数字滤波器完成了降噪过程。

高阶调制器包含更多积分器和反馈回路。例如，三阶调制器具有三个积分器和三个反馈回路。噪声整形函数通过降低 DC 附近的噪声并增加整形噪声，随调制器阶数的变化而变化。

高阶调制器以增加硅硬件、降低稳定性和信号范围为代价，提供了更高的性能。

ΔƩ 数字滤波器

ΔƩ ADC 在运行时采用了过采样 (OS)。过采样是调制器采样率 (F_S) 与 ADC 输出数据速率 (F_D) 之比，如公式 2 所示：

 公式 2

过采样通过使用低通数字滤波器，以数字方式限制经过噪声整形的数据的带宽，来改善 ΔƩ ADC 的噪声。

在 ΔƩ ADC 中，两个常用的数字滤波器是 sin(pf)/pf (sinc) 和线性相位有限冲激响应 (FIR) 滤波器。在 Texas Instruments 的 ADS1235 24 位 ΔƩ ADC、ADS1262 和 ADS1263 32 位 ΔƩ ADC（其中 ADS1263 集成了一个适用于背景测量的 24 位辅助 ΔƩ ADC）中，数字滤波器实现提供了以下选择：专门使用 sinc 滤波器，或使用 sinc 滤波器后跟 FIR 滤波器的组合（图 5）。

图 5：ADS1235 24 位 ΔƩ ADC 可以专门使用 sinc 滤波器，或使用 sinc 滤波器后跟 FIR 滤波器的组合。（图片来源：Texas Instruments）

在图 5 中，sinc（表示“Sinc”）滤波器是低通数字滤波器。sinc 滤波器的输出 (w(n)) 可使用公式 3 计算：

 公式 3

z 域传递函数为：

 公式 4

频率响应为：

 公式 5

在图 5 中，Sinc^N 等同于串联 N 个相同的 sinc 滤波器。sinc 滤波器的幅度与频率响应图形具有梳状外观（图 6）。

图 6：在每秒 2400 次采样 (SPS) 的 ADS1262/63 中，多个 sinc 数字滤波器产生了梳状频率响应；其中 sinc2 等效于串联两个相同的 sinc 滤波器，sinc3 等效于串联三个相同的 sinc 滤波器，依此类推。（图片来源：Texas Instruments）

在图 6 中，峰值和零点是 sinc 滤波器响应的特征。频率响应零点出现在 f (Hz) = N ·F_D，其中 N = 1, 2, 3, ...。在零频率处，滤波器的增益为零。

sinc 滤波器（串联）会增加衰减，导致延时增加。例如，如果在外部时钟速率为 7.3728 MHz 的特定 sinc 滤波器计算中，产生的输出数据速率为 14400 SPS，则第二个 sinc 滤波器的输出数据速率为 7200 SPS。

低通 FIR 滤波器是基于系数的滤波器。该滤波器具有 50 Hz 和 60 Hz 的同时衰减功能，以及 2.5 SPS 至 20 SPS 数据速率下的谐波功能。FIR 滤波器数据速率的转换延时相当于一个周期。FIR 滤波器从 sinc 滤波器接收经过预滤波的数据，并对数据进行抽取，以产生 10 SPS 的输出数据速率（图 7）。

图 7：在 ADS1262/63 中，FIR 滤波器可衰减 50 Hz 和 60 Hz 信号以降低线路频率干扰，并提供一系列靠近这些频率的响应零点。零点在 50 Hz 和 60 Hz 谐波处重复出现。（图片来源：Texas Instruments）

FIR 滤波器会衰减 50 Hz 和 60 Hz 信号以降低线路频率干扰，并提供一系列靠近这些频率的响应零点。响应零点在 50 Hz 和 60 Hz 谐波处重复出现。

精密的低噪声 ΔƩ ADC

先前提到的 Texas Instruments 的 ADS1235 差分输入 24 位转换器是低噪声 ΔƩ ADC 的极好例子。

ADS1235 是一款精密的 7200 SPS ΔƩ ADC，具有三个差分或五个单端输入，以及一个集成式可编程增益放大器 (PGA)，其增益包括 1、64 和 128。该器件还包括诊断功能，例如 PGA 超量程和参考监视器。该 ADC 为包括称重仪、应变片和电阻式压力传感器在内的高精度设备提供了高精度、零漂移的转换数据（图 8）。

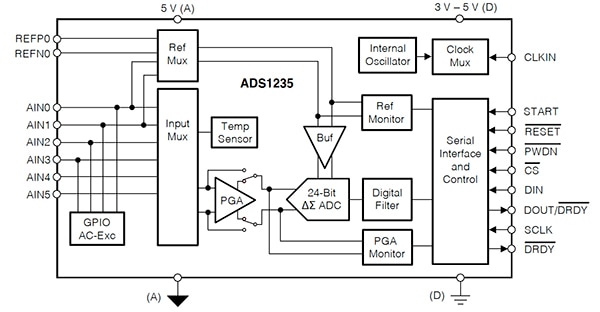图 8：具有六通道模拟输入和 GPIO 输入多路复用器的 ADS1235 24 位 ΔƩ ADC 方框图。（图片来源：Texas Instruments）

对于 ADS1235，影响噪声性能的重要因素包括数据速率、PGA 增益和斩波模式。数据速率较慢会在数字滤波器中引入转折频率，从而降低噪声。此外，由于在斩波模式下执行的两点数据平均化，与正常操作相比，噪声降低了 √2 倍。

在低频、2.5 SPS 数据速率和 1 V/V PGA 增益条件下，5 V 系统中的 sinc3 数字输出的转换器噪声为 0.15 mV_RMS（0.3 mV 峰峰值 (_PP)），有效分辨率为 24 位，无噪声分辨率为 24 位。该器件的理论和实际 SNR 均为 146 dB。事实上，在这些条件下，稳定的四阶调制器和 sinc1 至 sinc4 滤波器均可产生 24 位有效分辨率，以及 24 位无噪声分辨率。

ADS1235 已针对 2.5 SPS 数据速率实现了近乎完美的 24 位转换。此系列中的下一代 ΔƩ ADC 是 Texas Instruments 的 ADS1262/63。这些器件之间的主要区别在于 ADS1262/63 改善了低噪声电路，并提供了扩展的 32 位输出数据寄存器。

ADS1262/63 具有改进的低噪声 CMOS PGA，其增益包括 1、2、4、8、16 和 32。模拟前端 (AFE) 非常灵活，包含两个传感器激励电流源，非常适合直接 RTD 测量（图 9）。

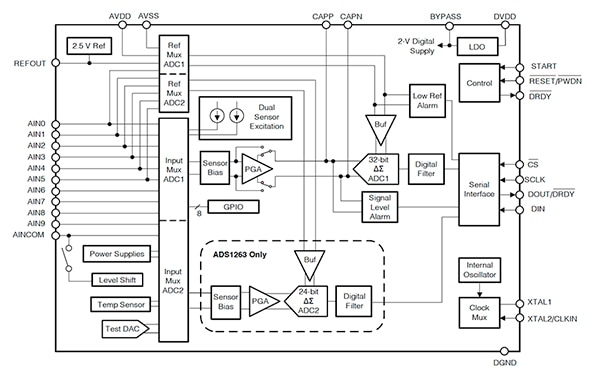图 9：具有十通道模拟输入多路复用器的 ADS1262 和 ADS1263 32 位 ΔƩ ADC 方框图。ADS1263 具有第二个片上 24 位 ΔƩ ADC。（图片来源：Texas Instruments）

与 ADS1235 一样，PGA 增益、数据速率、数字滤波器模式和斩波模式是影响 ADS1262/63 噪声性能的重要因素。ADS1262/63 具有 32 位分辨率，真正展现了低噪声深度功能。

首先，稳定的四阶调制器和 sinc1 至 sinc4 滤波器都能实现 32 位有效分辨率以及 24 位无噪声分辨率。通过配置低频率、2.5 SPS 数据速率和 1 V/V PGA 增益（已旁通），5 V 系统中的 sinc3 数字输出的转换器噪声仅为 0.08 mV_RMS (0.307 mV_PP)。该器件以 26.9 位超越了有效分辨率，以及 25 位无噪声分辨率。对于此 32 位系统，理论 SNR 为 387 dB，实际 SNR 等于 164 dB。

24 位和 32 位转换器的噪声之间区别非常明显，其中 32 位 ΔƩ ADC 的低噪声性能优于 24 位 ΔƩ ADC（表 2）。

*备注：SNR = 6.02 N + 1.76，其中 N 是位数

表 2：满量程输入电压 5 V 的 ADC RMS 噪声、峰峰值噪声和 SNR 的比较结果。（数据来源：Digi-Key Electronics）

总结

ΔƩ ADC 仍在不断增加功能，持续提升低噪声极限。本文介绍了如何将这种近乎数字化的低噪声 ADC 直接对应到温度、压力和测压元件应用中。在讨论精密型 24 位 ΔƩ ADC 和 32 位 ΔƩ ADC 的具体细节的同时，概括了实现超精密特性的途径。